2012 S2-09 Maths Blog
Monday, 8 October 2012
Sunday, 7 October 2012
Tuesday, 2 October 2012
Set Language and Notation Example 7
By : Jonathan Tan, Tan Yu Tao
The sets are categorized by the sides whether they are equal thus the square and rhombus are together intercepting and the rectangle and parallelogram are together intercepting.
Saturday, 29 September 2012
Tuesday, 25 September 2012
EOY Briefing
Here are some information about the paper:
Duration: 2 hr 30 min
Total marks: 100
40% of paper on Term 1 and 2 topics:
60% of paper on Term 3 and 4 topics:
Duration: 2 hr 30 min
Total marks: 100
40% of paper on Term 1 and 2 topics:
- Algebra and algebraic fractions
- Linear graphs
- Quadratic equations and graphs
- Area, perimeter, volume and surface area
- Pythagoras' Theorem
- Indices
60% of paper on Term 3 and 4 topics:
- Standard form
- Congruence and Similarity
- Area and volume of similar figures and solids
- Basic trigonometry
- Matrices
- Probability
- Simultaneous equations and graphs
- Set notation and venn diagrams
- Direct and inverse proportion
Monday, 24 September 2012
Set Theory - Task - A Visual Presentation and Recommendation
Mini Non-graded Performance Task : A Visual Presentation and Recommendation
You are the registrar of School of Science and Technology, Singapore (SST).
Since you have limited classrooms for classes, the school principal asked you to conduct a survey about the Applied Subjects you must offer for students.
Survey Results
After conducting a survey on 100 students, you obtained the following data:
40 students plan to enroll in Media Studies (M),
27 students prefer Fundamental of Electronic (F), and
23 students want to take Biotechnology (B).
Meanwhile 8 students prefer Media Studies (M) and Fundamental of Electronic (F),
10 students prefer Biotechnology (B) and Fundamental of Electronic (F), and
6 students prefer Biotechnology (B) and Media Studies (M), respectively.
Then you also found out that 5 students would like to enroll in all the three subjects, while 10 students prefer other subjects.
The principal required you to make a visual presentation of the data and a recommendation about the subjects to be offered.
Your presentation will be judged by the principal and the different department heads. Thus, make sure that it is clear, organized, accurate, and complete.
Venn diagram from oes_217
Wednesday, 19 September 2012
Tuesday, 18 September 2012
Independent Events
Independent Events
They are events and/or occurrences where the value and/or result of the previous similar event and/or occurrence does not affect the results obtained of the next event and/or occurrence.
For instance, when a die is rolled twice, the second roll is considered an independent event. This is so because the two rolls are separate incidences and the results of the second roll is only affected by the result of the first roll by such a minute amount that it is literally negligible.
Therefore, basically, Independent Events are just events that only has variables that directly affect it and not from a source that is linked to a previous random event. In other words, an event that is self-reliant.
Mini Task 4 *Proceed only if everything mentioned above is understood as the explanations will relate to above*
1(a) As mentioned earlier, a coin is relatively similar to a die, just that a coin has only 2 faces instead of the 6 faces on a die. Therefore, the event is an independent one.
(b) The event is the same as mentioned in the explanation above, just that a second die is added, thus, it still remains as an independent variable itself.
(c) This is a dependent variable as the probability of getting a king on the 3rd draw after the 2 aces , which were removed, is increased as compared to getting a king on the first draw since the number of total cards are reduced by 2, which increases the possibility of getting any card in the deck except for aces. Thus, the event is a dependent one.
(d) The explanation is somewhat similar to that is (c), where in order to have an increased chance of picking a white ball, the number of the red balls, which is the only other possible type of balls picked, should be reduced. In this case, the event fits the requirement of an increased chance in getting a white ball picked on the second draw. Thus, it is a dependent event.
Example 13
A coin only has two faces, heads and tails. Since there are only 3 coins and the probability to be calculated is having all 3 coins to have heads, we just take the number of possibilities and multiply it by itself the number of times the number of coins there are, which would give us a sample space of 8 different results. Since getting a heads, heads, heads is only possible in one scenario, we will be able to obtain the probability of 1/8.
Mini Task 5
They are events and/or occurrences where the value and/or result of the previous similar event and/or occurrence does not affect the results obtained of the next event and/or occurrence.
For instance, when a die is rolled twice, the second roll is considered an independent event. This is so because the two rolls are separate incidences and the results of the second roll is only affected by the result of the first roll by such a minute amount that it is literally negligible.
Therefore, basically, Independent Events are just events that only has variables that directly affect it and not from a source that is linked to a previous random event. In other words, an event that is self-reliant.
Mini Task 4 *Proceed only if everything mentioned above is understood as the explanations will relate to above*
1(a) As mentioned earlier, a coin is relatively similar to a die, just that a coin has only 2 faces instead of the 6 faces on a die. Therefore, the event is an independent one.
(b) The event is the same as mentioned in the explanation above, just that a second die is added, thus, it still remains as an independent variable itself.
(c) This is a dependent variable as the probability of getting a king on the 3rd draw after the 2 aces , which were removed, is increased as compared to getting a king on the first draw since the number of total cards are reduced by 2, which increases the possibility of getting any card in the deck except for aces. Thus, the event is a dependent one.
(d) The explanation is somewhat similar to that is (c), where in order to have an increased chance of picking a white ball, the number of the red balls, which is the only other possible type of balls picked, should be reduced. In this case, the event fits the requirement of an increased chance in getting a white ball picked on the second draw. Thus, it is a dependent event.
Example 13
A coin only has two faces, heads and tails. Since there are only 3 coins and the probability to be calculated is having all 3 coins to have heads, we just take the number of possibilities and multiply it by itself the number of times the number of coins there are, which would give us a sample space of 8 different results. Since getting a heads, heads, heads is only possible in one scenario, we will be able to obtain the probability of 1/8.
Mini Task 5
Probability Tree and Multiplication of probabilities
Probability Tree
What is a Tree Diagram?
A widely used diagram in solving probability problems which comprises of a number of branches. Each branch leads to an outcome in the sample space. In the tree diagram, all the possible outcomes are fair and equally likely to occur.
What is Probability Tree?
In independent events, when the probabilities of different events are not equal, the value of each probability has to be written on the respective branch of the tree. This tree is then called as probability tree. The 'branches' of a probability tree represent outcomes which are mutually exclusive.
What multiplication of probabilities?
It is needed when a outcome has 2 factors affecting the probability, a dependent event. Multiplication of the probabilities in both experiments with the same object is needed to find the overall probability.
An example would be calculating the probability of getting 6 as the first number and 3 as the second number when a 6 sided equal fair dice is being rolled 2 times.
First we will have to calculate the probability of getting 6 and 3 individually in each roll, which is also finding out the possibility of getting 6 as the outcome on the first roll.
After that we have to calculate the probability of getting 3 as the second number AFTER getting 6 as the first outcome. So we will have to multiply the possibility of getting 3 with the possibility of getting 6 as the first outcome.
So: (1/6)x(1/6)=(2/36)=(1/18)
Example 15
Mutually Exclusive
What is Mutually Exclusive?
Mutually exclusive outcomes are those that cannot happen at the same time. Which means, if A occurs, B has a zero percent chance of happening because of A happening. But this doesn't mean that another outcome such as C cannot happen.
Example: •One who turns left has a zero percent chance of turning right at that moment in time.
•One who flips a coin cannot get both heads and tails at the same time and can only get either heads or tails.
Example 11:
a.P(red)=2/9
b.P(red or green)=5/9
c.P(red green or blue)=9/9 = 1
Example 12:
a.P(4 or 5)= 1/14 + 2/7 = 5/14
b.P(4,5 or 6)=1
c. P(more than 6)= 1 - 1/14 - 2/7 - 3/7 = 3/14
Done by: Kang Xiong,Yong Jie,Bryan,Jasmine,Teri,Ada
Mutually exclusive outcomes are those that cannot happen at the same time. Which means, if A occurs, B has a zero percent chance of happening because of A happening. But this doesn't mean that another outcome such as C cannot happen.
Example: •One who turns left has a zero percent chance of turning right at that moment in time.
•One who flips a coin cannot get both heads and tails at the same time and can only get either heads or tails.
Example 11:
a.P(red)=2/9
b.P(red or green)=5/9
c.P(red green or blue)=9/9 = 1
Example 12:
a.P(4 or 5)= 1/14 + 2/7 = 5/14
b.P(4,5 or 6)=1
c. P(more than 6)= 1 - 1/14 - 2/7 - 3/7 = 3/14
Done by: Kang Xiong,Yong Jie,Bryan,Jasmine,Teri,Ada
Wednesday, 5 September 2012
Construction
Definition

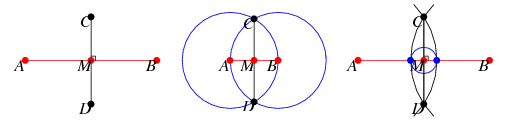
A perpendicular bisector

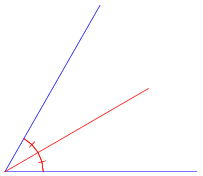
A. Constructing Perpendicular Bisector
B Angles Bisector
Google Form
Perpendicular Bisector

A perpendicular bisector  of a line segment
of a line segment  is a line segment perpendicular to
is a line segment perpendicular to 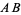 and passing through the midpoint
and passing through the midpoint 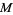 of
of 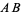 (left figure). The perpendicular bisector of a line segment can be constructed using a compass by drawing circles centered at
(left figure). The perpendicular bisector of a line segment can be constructed using a compass by drawing circles centered at 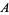 and
and 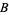 with radius
with radius 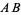 and connecting their two intersections. This line segment crosses
and connecting their two intersections. This line segment crosses 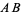 at the midpoint
at the midpoint 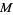 of
of 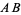 (middle figure). If the midpoint
(middle figure). If the midpoint 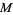 is known, then the perpendicular bisector can be constructed by drawing a small auxiliary circle around
is known, then the perpendicular bisector can be constructed by drawing a small auxiliary circle around 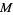 , then drawing an arc from each endpoint that crosses the line
, then drawing an arc from each endpoint that crosses the line 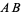 at the farthest intersection of the circle with the line (i.e., arcs with radii
at the farthest intersection of the circle with the line (i.e., arcs with radii 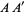 and
and 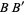 respectively). Connecting the intersections of the arcs then gives the perpendicular bisector
respectively). Connecting the intersections of the arcs then gives the perpendicular bisector 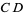 (right figure). Note that if the classical construction requirement that compasses be collapsible is dropped, then the auxiliary circle can be omitted and the rigid compass can be used to immediately draw the two arcs using any radius larger that half the length of
(right figure). Note that if the classical construction requirement that compasses be collapsible is dropped, then the auxiliary circle can be omitted and the rigid compass can be used to immediately draw the two arcs using any radius larger that half the length of 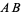 .Angle Bisector
.Angle Bisector

The (interior) bisector of an angle, also called the internal angle bisector (Kimberling 1998, pp. 11-12), is the line or line segment that divides the angle into two equal parts.
A. Constructing Perpendicular Bisector
B Angles Bisector
Google Form
Thursday, 30 August 2012
September Holidays Wednesday Remedial
P1 – 8:30 - 9:45
Topics: Direct and Inverse Constructions.
Compulsory
Strongly Recommended
Recommended
Not really recommended
Optional
Up to you
Topics: Direct and Inverse Constructions.
Compulsory
Strongly Recommended
Recommended
Not really recommended
Optional
Up to you
Monday, 20 August 2012
VIVA Yong Jie
1. What are my Key Learning points?
I have learned more in depth about the applications of the trigonometry ratios, making sure all of the items are checked and how to be focused in a task.
2. What have I understood about Trigonometry and Pythagoras Theorem as an applied learner?
I have understood that trigonometry and Pythagoras theorem are extremely connected to each other and that they could help solve and apply it in a every day problem.
Thursday, 16 August 2012
Tuesday, 14 August 2012
Level Test 4!!
1 Hour. <Quite a lot
Bring fulscap paper
Topics:
Standard Forms
Similarity (Figures + Solids)
Congruency (4 tests AAA, ASA, SAS, RHS)
Pythagoras Theorem (its PY-THA-GO-RAS)
Trigonometry
Matrices
Good Luck
Bring fulscap paper
Topics:
Standard Forms
Similarity (Figures + Solids)
Congruency (4 tests AAA, ASA, SAS, RHS)
Pythagoras Theorem (its PY-THA-GO-RAS)
Trigonometry
Matrices
Good Luck
Sunday, 12 August 2012
Matrices
Notes
Matrices And Application Of Matrices from mailrenuka
Matrices Concept map
source: http://faculty.oxy.edu/ron/math/214/Concept%20Map/Matrices.html
Matrices Concept map
source: http://faculty.oxy.edu/ron/math/214/Concept%20Map/Matrices.html
Matrices
The following shows the application of matrices in the Real World.
Questions for you to comment and post in this blog.
.1 What are the characteristics of the information presented in Sample A to E
.2 How is this information be made relevant and easy to use for the people?
.3 Define mathematics: MATRICES
.4 Give one other examples on how Matrices is used.
SAMPLE A
Questions for you to comment and post in this blog.
.1 What are the characteristics of the information presented in Sample A to E
.2 How is this information be made relevant and easy to use for the people?
.3 Define mathematics: MATRICES
.4 Give one other examples on how Matrices is used.
SAMPLE A
SAMPLE B
http://www.sbstransit.com.sg/transport/trpt_bus_timetable.aspx
SAMPLE C
http://www.lrta.gov.ph/tickets_fares.htm
SAMPLE D
http://www.london2012.com/medals/medal-count/
SAMPLE E
Subscribe to:
Posts (Atom)





























